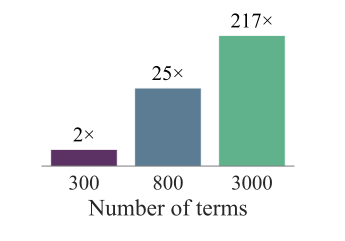Publications tagged "computational-algebra"
- PreprintarXiv preprint arXiv:2510.13444 2025
Certifying nonnegativity of polynomials is a well-known NP-hard problem with direct applications spanning non-convex optimization, control, robotics, and beyond. A sufficient condition for nonnegativity is the Sum of Squares (SOS) property, i.e., it can be written as a sum of squares of other polynomials. In practice, however, certifying the SOS criterion remains computationally expensive and often involves solving a Semidefinite Program (SDP), whose dimensionality grows quadratically in the size of the monomial basis of the SOS expression; hence, various methods to reduce the size of the monomial basis have been proposed. In this work, we introduce the first learning-augmented algorithm to certify the SOS criterion. To this end, we train a Transformer model that predicts an almost-minimal monomial basis for a given polynomial, thereby drastically reducing the size of the corresponding SDP. Our overall methodology comprises three key components: efficient training dataset generation of over 100 million SOS polynomials, design and training of the corresponding Transformer architecture, and a systematic fallback mechanism to ensure correct termination, which we analyze theoretically. We validate our approach on over 200 benchmark datasets, achieving speedups of over 100× compared to state-of-the-art solvers and enabling the solution of instances where competing approaches fail. Our findings provide novel insights towards transforming the practical scalability of SOS programming.
@article{pelleriti2025neural, title = {Neural Sum-of-Squares: Certifying the Nonnegativity of Polynomials with Transformers}, author = {Pelleriti, Nico and Spiegel, Christoph and Liu, Shiwei and Mart{\'i}nez-Rubio, David and Zimmer, Max and Pokutta, Sebastian}, journal = {arXiv preprint arXiv:2510.13444}, year = {2025}, } - H. Kera, N. Pelleriti, Y. Ishihara, M. Zimmer, and S. PokuttaNEURIPS25 Advances in Neural Information Processing Systems 2025
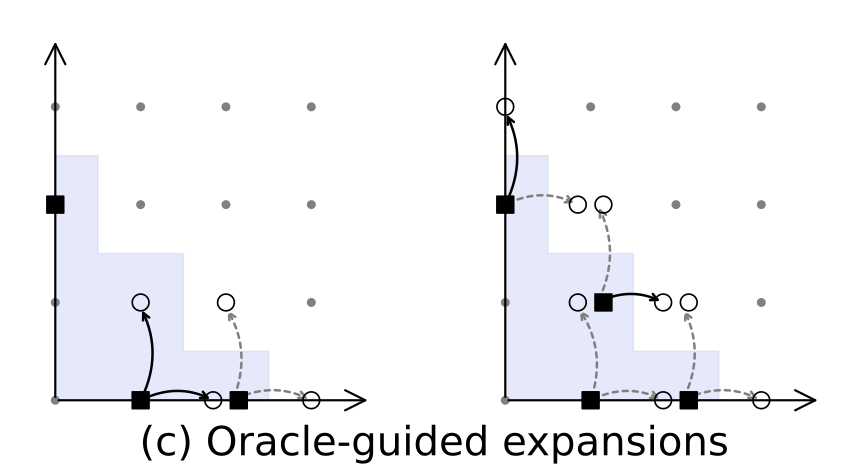
Solving systems of polynomial equations, particularly those with finitely many solutions, is a crucial challenge across many scientific fields. Traditional methods like Gröbner and Border bases are fundamental but suffer from high computational costs, which have motivated recent Deep Learning approaches to improve efficiency, albeit at the expense of output correctness. In this work, we introduce the Oracle Border Basis Algorithm, the first Deep Learning approach that accelerates Border basis computation while maintaining output guarantees. To this end, we design and train a Transformer-based oracle that identifies and eliminates computationally expensive reduction steps, which we find to dominate the algorithm’s runtime. By selectively invoking this oracle during critical phases of computation, we achieve substantial speedup factors of up to 3.5x compared to the base algorithm, without compromising the correctness of results. To generate the training data, we develop a sampling method and provide the first sampling theorem for border bases. We construct a tokenization and embedding scheme tailored to monomial-centered algebraic computations, resulting in a compact and expressive input representation, which reduces the number of tokens to encode an n-variate polynomial by a factor of O(n). Our learning approach is data efficient, stable, and a practical enhancement to traditional computer algebra algorithms and symbolic computation.
@inproceedings{kera2025computationalalgebraattentiontransformer, title = {Computational Algebra with Attention: Transformer Oracles for Border Basis Algorithms}, author = {Kera, Hiroshi and Pelleriti, Nico and Ishihara, Yuki and Zimmer, Max and Pokutta, Sebastian}, booktitle = {Advances in Neural Information Processing Systems}, volume = {38}, year = {2025}, } - N. Pelleriti, M. Zimmer, E. Wirth, and S. PokuttaICML25 Forty-second International Conference on Machine Learning 2025
Deep neural networks have reshaped modern machine learning by learning powerful latent representations that often align with the manifold hypothesis: high-dimensional data lie on lower-dimensional manifolds. In this paper, we establish a connection between manifold learning and computational algebra by demonstrating how vanishing ideals can characterize the latent manifolds of deep networks. To that end, we propose a new neural architecture that (i) truncates a pretrained network at an intermediate layer, (ii) approximates each class manifold via polynomial generators of the vanishing ideal, and (iii) transforms the resulting latent space into linearly separable features through a single polynomial layer. The resulting models have significantly fewer layers than their pretrained baselines, while maintaining comparable accuracy, achieving higher throughput, and utilizing fewer parameters. Furthermore, drawing on spectral complexity analysis, we derive sharper theoretical guarantees for generalization, showing that our approach can in principle offer tighter bounds than standard deep networks. Numerical experiments confirm the effectiveness and efficiency of the proposed approach.
@inproceedings{pelleriti2025approximatinglatentmanifoldsneural, title = {Approximating Latent Manifolds in Neural Networks via Vanishing Ideals}, author = {Pelleriti, Nico and Zimmer, Max and Wirth, Elias and Pokutta, Sebastian}, booktitle = {Forty-second International Conference on Machine Learning}, year = {2025}, url = {https://openreview.net/forum?id=WYlerYGDPL}, }