Publications tagged "optimization"

Minimizing gradients of a convex function is an important problem across optimization and learning tasks. The gradient provides a directly computable certificate of approximate stationarity, and its minimization usually implies stronger results than those for minimization of function values. In this work, we study gradient-norm minimization for convex functions that are (L,κ)-Hölder smooth with respect to the \ell_p-norms, p ≥1. We develop algorithms that achieve near-optimal gradient-oracle complexity for this problem. In the smooth case, our results resolve the previously open setting p>2. For Hölder-smooth objectives, we close the complexity gap throughout the full p-range, including to the best of our knowledge, a gap in the Euclidean case. We provide two families of algorithms: the first one comes with a simple iteration and generalizes a phenomenon known as mirror duality, exploiting dual behaviours of algorithms with errors and inexact computations. The second makes use of accumulating regularizers centered at different approximate solutions, which we sequentially minimize in order to provide our near-optimal rates.

We present a constructive lower bound demonstrating that Frank-Wolfe optimization requires Ω(1/√ε) iterations when both the objective function and constraint set possess smoothness and strong convexity. This result confirms that existing convergence guarantees of O(1/√ε) are optimal. We focus on a representative problem: minimizing a strongly convex quadratic over a Euclidean unit ball with the optimizer positioned at the boundary. We introduce a novel computational method for constructing worst-case trajectories and provide an analytical proof establishing our theoretical bound.

This article investigates the interplay of rounding objective coefficients in binary programs and almost symmetries. Empirically, reducing the number of significant bits through rounding often leads to instances that are easier to solve. One reason can be that the amount of symmetries increases, which enables solvers to be more effective when they are exploited. This can signify that the original instance contains ’almost symmetries’. Furthermore, solving the rounded problems provides approximations to the original objective values. We empirically investigate these relations on instances of the capacitated facility location problem, the knapsack problem and a diverse collection of additional instances, using the solvers SCIP and CP-SAT. For all investigated problem classes, we show empirically that this yields faster algorithms with guaranteed solution quality. The influence of symmetry depends on the instance type and solver.

Pruning is a common technique to reduce the compute and storage requirements of Neural Networks. While conventional approaches typically retrain the model to recover pruning-induced performance degradation, state-of-the-art Large Language Model (LLM) pruning methods operate layer-wise, minimizing the per-layer pruning error on a small calibration dataset to avoid full retraining, which is considered computationally prohibitive for LLMs. However, finding the optimal pruning mask is a hard combinatorial problem and solving it to optimality is intractable. Existing methods hence rely on greedy heuristics that ignore the weight interactions in the pruning objective. In this work, we instead consider the convex relaxation of these combinatorial constraints and solve the resulting problem using the Frank-Wolfe (FW) algorithm. Our method drastically reduces the per-layer pruning error, outperforms strong baselines on state-of-the-art GPT architectures, and remains memory-efficient. We provide theoretical justification by showing that, combined with the convergence guarantees of the FW algorithm, we obtain an approximate solution to the original combinatorial problem upon rounding the relaxed solution to integrality.

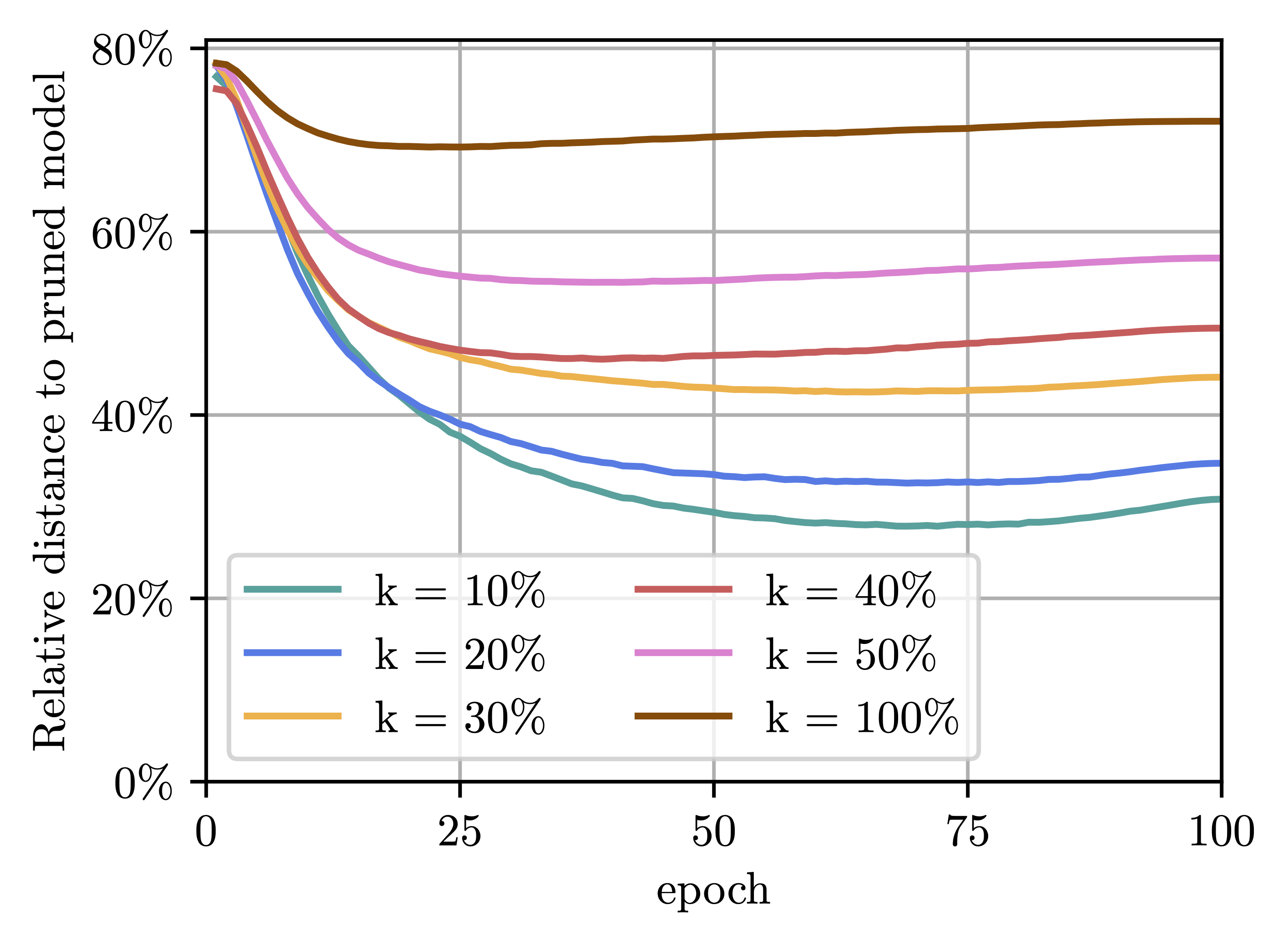
Many existing Neural Network pruning approaches either rely on retraining to compensate for pruning-caused performance degradation or they induce strong biases to converge to a specific sparse solution throughout training. A third paradigm obtains a wide range of compression ratios from a single dense training run while also avoiding retraining. Recent work of Pokutta et al. (2020) and Miao et al. (2022) suggests that the Stochastic Frank-Wolfe (SFW) algorithm is particularly suited for training state-of-the-art models that are robust to compression. We propose leveraging k-support norm ball constraints and demonstrate significant improvements over the results of Miao et al. (2022) in the case of unstructured pruning. We also extend these ideas to the structured pruning domain and propose novel approaches to both ensure robustness to the pruning of convolutional filters as well as to low-rank tensor decompositions of convolutional layers. In the latter case, our approach performs on-par with nuclear-norm regularization baselines while requiring only half of the computational resources. Our findings also indicate that the robustness of SFW-trained models largely depends on the gradient rescaling of the learning rate and we establish a theoretical foundation for that practice.

This study examines the connection between an agent-based transport simulation and Nash flows over time. While the former is able to represent many details of traffic and model large-scale, real-world traffic situations with a co-evolutionary approach, the latter provides an environment for provable mathematical statements and results on exact user equilibria. The flow dynamics of both models are very similar with the main difference that the simulation is discrete in terms of vehicles and time while the flows over time model considers continuous flows and continuous time. This raises the question whether Nash flows over time are the limit of the convergence process when decreasing the vehicle and time step size in the simulation coherently. The experiments presented in this study indicate this strong connection which provides a justification for the analytical model and a theoretical foundation for the simulation.

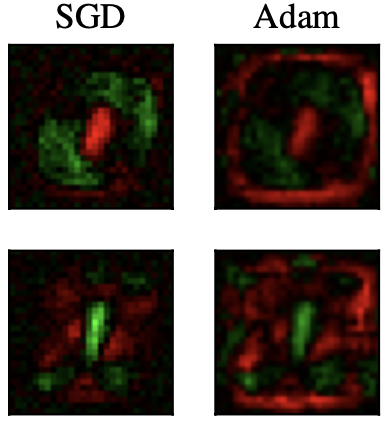
This paper studies the empirical efficacy and benefits of using projection-free first-order methods in the form of Conditional Gradients, a.k.a. Frank-Wolfe methods, for training Neural Networks with constrained parameters. We draw comparisons both to current state-of-the-art stochastic Gradient Descent methods as well as across different variants of stochastic Conditional Gradients. In particular, we show the general feasibility of training Neural Networks whose parameters are constrained by a convex feasible region using Frank-Wolfe algorithms and compare different stochastic variants. We then show that, by choosing an appropriate region, one can achieve performance exceeding that of unconstrained stochastic Gradient Descent and matching state-of-the-art results relying on L^2-regularization. Lastly, we also demonstrate that, besides impacting performance, the particular choice of constraints can have a drastic impact on the learned representations.